[C++] 다익스트라 알고리즘

 

다익스트라 알고리즘은 음의 가중치가 없는 그래프의 한 노드에서 다른 모든 노드까지의 최단거리를 구하는 알고리즘이다. 

음의 가중치가 있는 그래프의 경우 벨만 포드 알고리즘을 사용하여야 한다.

우선순위 큐를 이용하여 다음과 같이 간단하게 구현할 수 있다.

#include <iostream>
#include <vector>
#include <queue>
#define MAX 100
#define INF 987654321
using namespace std;

vector <pair <int, int>> nodes[MAX];
int dist[MAX];
priority_queue <pair <int, int>> pq;

void Dijkstra(int start) {
    dist[start] = 0;
    pq.push({0, start});

    while(!pq.empty()) {
        int len = -pq.top().first;
        int cur = pq.top().second;
        pq.pop();
        
        if (dist[cur] < len)
            continue;
        
        for (int i = 0; i < nodes[cur].size(); ++i) {
            int nLen = len + nodes[cur][i].first;
            int next = nodes[cur][i].second;
            if (dist[next] > nLen) {
                dist[next] = nLen;
                pq.push({-nLen, next});
            }
        }
    }

    return;
}

void createNode(int start, int end, int len) {
    nodes[start].push_back({len, end});
    nodes[end].push_back({len, start});
    return;
}

void init() {
    for (int i = 0; i < MAX; ++i)
        dist[i] = INF;

    createNode(1, 4, 7);
    createNode(1, 3, 6);
    createNode(1, 2, 3);
    createNode(2, 3, 1);
    createNode(3, 4, 1);
    return;
}

int main() { 
    init();
    Dijkstra(1);

    for (int i = 1; i <= 4; ++i)
        cout << dist[i] << " ";
}

 

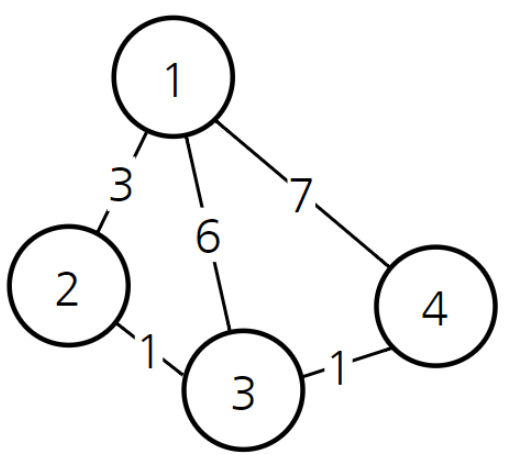
그래프가 위와 같이 생성되었고, 1번 노드 기준으로 다른 노드에 대한 최단거리를 구한다고 했을 때, 

1, 2, 3, 4번 노드에 대하여 각각 0, 3, 4, 5로 잘 구해지는 것을 확인할 수 있다.